Proračun kapaciteta kondenzatora

Kapacitet C je kapacitet kondenzatora da prihvati (pohrani i zadrži) količinu elektriciteta Q u amper-sekundama ili naboj Q u privjescima. Ako tijelu, na primjer lopti, kažete električni naboj (količinu elektriciteta) Q, tada će elektroskop spojen između tog tijela i zemlje pokazati napon U (slika 1). Taj je napon proporcionalan naboju, a također ovisi o obliku i veličini tijela.

Odnos između naboja Q i napona U izražava se formulom Q = C ∙ U.

Konstanta proporcionalnosti C naziva se kapacitivnost tijela. Ako tijelo ima oblik lopte, kapacitet tijela je proporcionalan polumjeru lopte r.

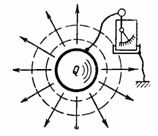
Riža. 1.

Mjerna jedinica za kapacitet je farad (F).

Tijelo ima kapacitet od 1 F kada naboj od 1 k proizvede napon od 1 V. između njega i zemlje. Faradi su vrlo velika mjerna jedinica pa se u praksi koriste manje jedinice: mikrofarad (μF), nanofarad (nF) i pikofarad (pF)...

Ove jedinice su povezane sljedećim omjerima: 1 F = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Kapacitet kuglice polumjera 1 cm je 1,1 pF.

Ne samo izolirano tijelo može akumulirati naboj, već i poseban uređaj koji se zove kondenzator. Kondenzator se sastoji od dvije ili više ploča (ploča) koje su odvojene dielektrikom (izolacijom).

Na sl. Slika 2 prikazuje krug s istosmjernim izvorom spojenim na kondenzator. Kada je uključen, na desnoj ploči kondenzatora stvara se pozitivan naboj +Q, a na lijevoj negativni naboj –Q. Tijekom naboj kondenzatora kroz krug teče struja koja prestaje nakon završetka punjenja; tada će napon na kondenzatoru biti jednak e. itd. c. izvor U. Naboj na ploči kondenzatora, napon i kapacitet povezani su omjerom Q = C ∙ U. U tom slučaju u dielektriku kondenzatora nastaje elektrostatsko polje.

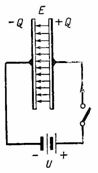
Riža. 2.

Kapacitet kondenzatora sa zračnim dielektrikom može se izračunati po formuli C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, gdje je S površina jedne ploče, cm2; d je udaljenost između ploča, cm; C je kapacitet kondenzatora, pF.

Kapacitet kondenzatora koji se sastoji od n ploča (slika 3) jednak je: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

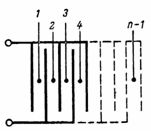
Riža. 3.

Ako se prostor između ploča ispuni drugim dielektrikom, primjerice papirom, kapacitet kondenzatora povećat će se za faktor ε. Kada se koristi papirna izolacija, kapacitet će se povećati 3 puta, s izolacijom od tinjca - 5-8 puta, sa staklom - 7 puta itd. Vrijednost ε naziva se dielektrična konstanta dielektrika.

Opća formula za određivanje kapaciteta kondenzatora s dielektričnom konstantom ε (epsilon) je: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Ova formula je korisna za izračun malih promjenjivih kondenzatora za radio.Ista se formula može prikazati kao: C = (ε_0 ∙ ε ∙ S) / d, gdje je ε_0 dielektrična konstanta ili dielektrična konstanta vakuuma (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε je dielektrična konstanta dielektrika.

U ovoj se formuli dimenzije zamjenjuju u metrima, a kapacitivnost se dobiva u faradima.

Primjeri za

1. Koliki je kapacitet planete Zemlje čiji je polumjer r = 6378 km?

Budući da je kapacitet kugle polumjera 1 cm jednak 1,11 pF, kapacitet Zemlje je: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Kapacitet kuglice veličine našeg planeta je relativno malen. Taj kapacitet imaju mali elektrolitski kondenzatori).

2. Odredite kapacitet kondenzatora koji se sastoji od dvije ploče od kojih svaka ima površinu S = 120 cm2.

Ploče su odvojene slojem zraka debljine d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF .. .

3. Odredite kapacitet kondenzatora prema podacima iz prethodnog primjera, ako je prostor između ploča ispunjen voštanim papirom dielektrične konstante ε = 4, staklom (ε = 7), elektro kartonom (ε = 2) , tinjac (ε = 8 ).

Kondenzator od voštanog papira ima kapacitet C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Kapacitet staklenog kondenzatora je C = 7 ∙ 21,2 = 148,4 pF.

Kapacitet kartonskog kondenzatora je C = 2 ∙ 21,2 = 42,3 pF.

Kapacitet tinjčevog kondenzatora je C = 8 ∙ 21,2 = 169,6 pF.

4. Koliki je kapacitet zračnog rotacijskog kondenzatora za radio prijamnik koji se sastoji od 20 ploča površine 20 cm2 ako je razmak između ploča 0,06 cm (slika 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondenzator prikazan na Sl.3, sastoji se od zasebnih najjednostavnijih kondenzatora s dvije ploče, čiji je broj jednak n-1.

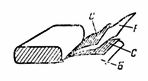
5. Papirnati kondenzator kapaciteta C = 2 μF sastoji se od dvije trake staniola C i dvije trake dielektrika od voštanog papira B dielektrične konstante ε = 6. Debljina voštanog papira je d = 0,1 mm. Presavijene trake se smotaju, povoci se izrađuju od čeličnih ploča. Odredite duljinu čelične trake kondenzatora ako je njezina širina 4 cm (slika 4).

Riža. 4.

Prvo odredimo površinu jedne trake formulom C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, odakle je S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Duljina svake trake je l = 37680/4 = 9420 cm = 94,2 m.