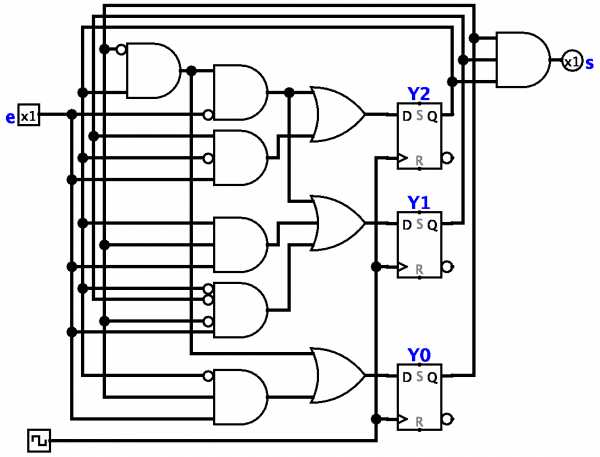
Teorija automata, konačni automati
Struktura, dizajn, princip rada raznih strojeva uvelike su određeni njegovom funkcionalnom svrhom. Razlikovati tehnološke, prometne, računalne, vojne i druge strojeve. Cjelokupni automatski kompleksi dizajnirani za izvođenje složenih tehnoloških procesa naširoko su uvedeni u razne industrije. Automati su projektirani i izgrađeni koji obavljaju različite logičke funkcije (logički strojevi).
Teorija automata — kibernetička sekcija, koji je nastao pod utjecajem zahtjeva tehnologije digitalnih računala i upravljačkih strojeva. Diskretni automati koji se proučavaju u teoriji automata su apstraktni modeli stvarnih sustava (tehničkih i bioloških) koji obrađuju diskretne (digitalne) informacije u diskretnim vremenskim koracima.
Teorija automata temelji se na preciznim matematičkim konceptima koji formaliziraju intuitivne ideje o funkcioniranju (ponašanju) automata io njegovoj strukturi (unutarnjoj strukturi).
Pritom se pod informacijskom transformacijom uvijek podrazumijeva operacija koja transformira ulazne nizove sastavljene od slova ulazne abecede u izlazne nizove sastavljene od slova izlazne abecede.
Široko se koristi aparatura matematičke logike, algebre, teorije vjerojatnosti, kombinatorike i teorije grafova.
Problem s teorijom automata u nekim njezinim dijelovima (strukturna teorija automata) je rastao iz teorije relejno-kontaktnih sklopova, koji se počeo oblikovati krajem 1930-ih. uključivo metode logičke algebre.

U strukturnoj teoriji automata proučavaju se različite vrste shema, osmišljenih da opisuju kako se složeni automat stvara od jednostavnijih komponenti (elemenata) pravilno povezanih u sustav.
Drugi smjer, nazvan apstraktna teorija automata, proučava ponašanje automata (to jest, prirodu transformacije informacija koju oni provode), dok se apstrahira od specifičnosti njihove unutarnje strukture, a nastao je 1950-ih.
U okviru apstraktne teorije automata, sadržaj pojmova "automat" i "stroj" u biti se iscrpljuje standardnim opisom transformacije informacija koju provodi automat. Takva transformacija može biti deterministička, ali može biti i probabilističke prirode.
Najviše se proučavaju deterministički strojevi (automati), koji uključuju konačne automate — glavni predmet proučavanja u teoriji automata.
Konačni automat karakterizira ograničena količina memorije (broj unutarnjih stanja) i definiran je pomoću prijelazne funkcije.Uz nešto razumne idealizacije, svi moderni matematički strojevi, pa čak i mozak, sa stajališta njihova funkcioniranja, mogu se smatrati konačnim automatima.
Pojmovi "sekvencijalni stroj", "Millyjev automat", "Mooreov automat" koriste se u literaturi (i to ne svi autori jedinstveno) kao sinonimi pojma "konačni automat" ili za naglašavanje određenih značajki u prijelaznim funkcijama konačnog automata. automat.
Automati s neograničenom memorijom Turingov je stroj sposoban izvesti (potencijalno) bilo kakvu učinkovitu transformaciju informacija. Koncept "Turingovog stroja" nastao je prije koncepta "konačnog stroja" i uglavnom se proučava u teoriji algoritama.
Teorija apstraktnih automata usko je povezana s dobro poznatim algebarskim teorijama, na primjer teorijom polugrupa. S primijenjenog gledišta zanimljivi su rezultati koji karakteriziraju transformaciju informacija u automatu u smislu veličine memorije.
To je slučaj, na primjer, u problemima s eksperimentima na automatima (radovi E.F. Moorea i dr.), gdje se jedna ili druga informacija o prijelaznim funkcijama automata ili o kapacitetu njegove memorije dobiva iz rezultata eksperimenti.
Drugi zadatak je izračunati periode izlaznih sekvenci, na temelju dostupnih informacija o veličini memorije automata i periodima ulaznih sekvenci.
Od velike je važnosti razvoj metoda za minimiziranje memorije konačnih automata i proučavanje njihovog ponašanja u slučajnim okruženjima.
U teoriji apstraktnih automata, problem sinteze je sljedeći.U terminima nekog jasno formaliziranog jezika, napisani su uvjeti za ponašanje dizajniranog automata (za događaj predstavljen u automatu). U tom slučaju potrebno je razviti metode koje prema svakom napisanom uvjetu:
1) saznati postoji li takav stroj stanja da informacija koju on transformira ispunjava ovaj uvjet;
2) ako da, tada se konstruiraju prijelazne funkcije takvog konačnog stroja ili se procjenjuje njegova veličina memorije.
Rješenje zadatka sinteze u takvoj formulaciji pretpostavlja preliminarno stvaranje prikladnog jezika za snimanje uvjeta rada automata s prikladnim algoritmima za prijelaz sa snimanja na tranzitivne funkcije.
U strukturnoj teoriji automata, problem sinteze sastoji se u konstruiranju lanca elemenata danog tipa koji realizira konačni automat zadan njegovim prijelaznim funkcijama. U tom slučaju obično navode neki kriterij optimalnosti (na primjer, minimalni broj elemenata) i nastoje dobiti optimalnu shemu.
Kako se kasnije pokazalo, to znači da su neke metode i koncepti razvijeni ranije u vezi s relejnim kontaktnim krugovima primjenjivi na krugove drugog tipa.
U vezi s razvojem elektroničkih tehnologija, najraširenije su sheme funkcionalnih elemenata (logičke mreže). Poseban slučaj logičkih mreža su apstraktne neuronske mreže, čiji se elementi nazivaju neuroni.
Razvijene su mnoge metode sinteze ovisno o vrsti sklopova i transformaciji informacija za koje su namijenjeni (Sinteza relejnih uređaja).
pogledaj -Minimizacija kombinacijskih sklopova, Carnotova preslikavanja, sinteza sklopova
Konačni stroj — matematički model upravljačkog sustava s fiksnom veličinom memorije (koja se ne može povećavati tijekom rada).
Koncept konačnog stroja je matematička apstrakcija koja karakterizira opće karakteristike skupa upravljačkih sustava (na primjer, relejni uređaj s više petlji). Svi takvi sustavi imaju zajedničke značajke koje je prirodno prihvatiti kao definiciju konačnog automata.
Svaki završeni automat ima ulaz izložen vanjskim utjecajima i unutarnjim elementima. I za ulazne i za unutarnje elemente postoji fiksni broj diskretnih stanja koja mogu poprimiti.
Promjena stanja ulaznih i unutarnjih elemenata događa se u diskretnim trenucima vremena, intervali između kojih se nazivaju tikovi. Unutarnje stanje (stanje unutarnjih dijelova) na kraju vrpce u potpunosti je određeno unutarnjim stanjem i stanjem ulaza na početku vrpce.
Sve druge definicije konačnog automata mogu se svesti na ovu karakteristiku, posebice definicije koje pretpostavljaju da konačni automat ima izlaz koji ovisi o unutarnjem stanju automata u danom trenutku.
U smislu takve karakteristike, priroda njegovih ulaza i unutarnjih stanja je irelevantna za opis potpunog automata. Umjesto unosa i stanja, možete samo pogledati njihove brojeve u nasumičnim numeriranjem.
Automat stanja bit će postavljen ako je specificirana ovisnost njegovog internog broja stanja o prethodnom internom broju stanja i prethodnom ulaznom broju stanja. Takav zadatak može biti u obliku završne tablice.
Drugi uobičajeni način definiranja potpunog automata je konstrukcija tzv prijelazni dijagrami. Ulazna stanja često se jednostavno nazivaju ulazima, a interna stanja su jednostavno stanja.
Konačni automat može biti model kako tehničkih uređaja tako i nekih bioloških sustava. Automati prve vrste su, na primjer, relejni uređaji i različita elektronička računala, uklj. programabilni logički kontroleri.
U slučaju relejnog uređaja, ulogu ulaznih stanja igraju kombinacije stanja osjetljivih elemenata relejnog uređaja (svaka kombinacija takvih stanja je «složeno stanje», karakterizirano indikacijom svih osjetljivih elemenata ta diskretna stanja koja imaju u danom trenutku). Slično, kombinacije stanja međuelemenata relejnog uređaja djeluju kao interna stanja.
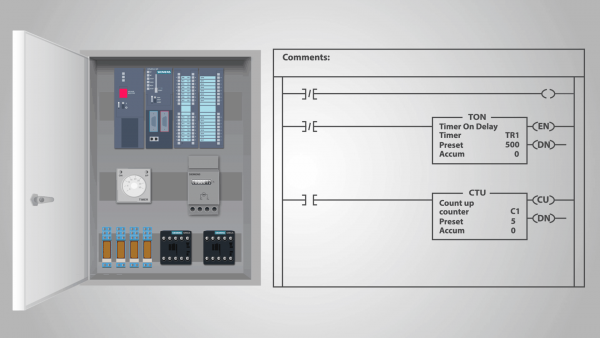
Programabilni logički kontroler (PLC) primjer je relejnog uređaja koji se može nazvati samostalnim strojem stanja.
Naime, nakon što je program unesen u PLC i kontroler je počeo računati, on nije izložen vanjskim utjecajima i svako sljedeće stanje je potpuno određeno njegovim prethodnim stanjem. Možemo pretpostaviti da ulaz ima isto stanje u svakom taktu.
Obrnuto, svaki konačni stroj koji ima jedino moguće ulazno stanje prirodno se naziva autonomnim, jer u ovom slučaju vanjska okolina ne nosi informacije koje kontroliraju njegovo ponašanje.
Vidi također:
Primjena mikroprocesorskih sustava u elektrotehnici na primjeru primjene PLC-a