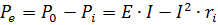Bilanca snaga u električnom krugu
Prema Joule-Lenzov zakon rad istosmjerne struje u otporu,
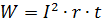
Ako se u razmatranu granu umjesto otpornika uključi neki drugi pretvarač elektromagnetske energije u mehaničku ili kemijsku ili neki drugi oblik energije (elektromotor, baterija za punjenje itd.), rad struje tijekom vremena t može se izračunati u slučaj da ako je poznat napon pretvarača.
U ovom slučaju Joule-Lenzova formula ima drugačiji oblik:
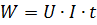
Pri istosmjernoj struji, snaga koja se dovodi u dio kruga s otporom r dana je izrazom:
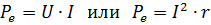
gdje I, U i r zadržavaju isto značenje kao u Joule-Lenzovoj formuli.
Snaga potrošena u cijelom vanjskom krugu i snaga koju daje generator su iste. Snaga koju razvija generator uvijek je veća od one koju generator daje vanjskom krugu, jer se dio snage troši za pokrivanje gubitaka unutar samog generatora.
Izraz za bilancu snage za jednu zatvorenu petlju koja sadrži generator s emf E i unutarnjim otporom ri i otpornik otpora r može se dobiti iz Kirchhoffove jednadžbe.
Za ovaj sklop
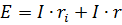
Ako se obje strane ove jednadžbe pomnože sa strujom u krugu, tada će rezultirajuća jednadžba predstavljati ravnotežu snage u tom krugu
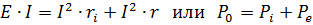
Snaga koju razvija generator jednaka je zbroju snage izgubljene unutar generatora i predane vanjskom krugu. P0 = EI je snaga koju razvija generator, Pe = UI = I2r je snaga koju generator daje vanjskom krugu, a Pi — I2ri je snaga izgubljena unutar samog generatora.
Pri odabiru istih pozitivnih smjerova struje kroz dvostrani priključak I i napon dvostranog priključka U, snaga koju troše dva priključka, odnosno korisničko sučelje proizvoda, mora biti pozitivna. Ako se istovremeno pokaže da je korisničko sučelje proizvoda negativno, to će značiti da uređaj s dva terminala ne troši elektromagnetsku energiju, već je naprotiv generator elektromagnetske energije i tu energiju predaje strujni krug.
Ako u električnom krugu više uređaja s dva priključka emitira elektromagnetsku energiju u krug, ostali apsorbiraju tu energiju. U krugu istosmjerne struje ne može doći do nakupljanja elektromagnetske energije. Dakle, zbroj snage potrošene u pasivnim mrežama s dva priključka i snage izgubljene unutar generatora mora biti jednak algebarskom zbroju snaga koje razvijaju svi generatori, tj. zbroj proizvoda EkIk svih generatora koji rade u krugu:
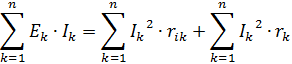
gdje je n — broj grana u lancu.
Jednadžba ravnoteže dobivena za jednostavan krug koji sadrži jedan generator može se prepisati izražavanjem potrošene snage u vanjskom krugu kao snage koju izražava generator i snage izgubljene unutar generatora: