Zakon održanja energije

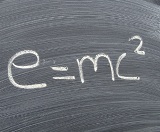Moderna fizika poznaje mnoge vrste energije povezane s gibanjem ili različitim međusobnim rasporedom najrazličitijih materijalnih tijela ili čestica, npr. svako tijelo koje se kreće ima kinetičku energiju proporcionalnu kvadratu svoje brzine. Ta se energija može promijeniti ako se brzina tijela povećava ili smanjuje. Tijelo podignuto iznad tla ima gravitacijsku potencijalnu energiju koja varira u tri promjene visine tijela.

Stacionarni električni naboji koji su međusobno na određenoj udaljenosti imaju elektrostatsku potencijalnu energiju u skladu s činjenicom da se, prema Coulombovom zakonu, naboji ili privlače (ako su različitih predznaka) ili odbijaju silom obrnuto proporcionalnom kvadratu udaljenost između njih.

Kinetičku i potencijalnu energiju posjeduju molekule, atomi i čestice, njihovi sastojci — elektroni, protoni, neutroni itd. u obliku mehaničkog rada, u protjecanju električne struje, u prijenosu topline, u promjeni unutarnjeg stanja tijela, u širenju elektromagnetskih valova itd.

Prije više od 100 godina uspostavljen je temeljni zakon fizike prema kojem energija ne može nestati niti nastati ni iz čega. Ona samo može prelaziti iz jednog tipa u drugi... Taj se zakon naziva zakon održanja energije.

U djelima A. Einsteina ovaj je zakon značajno razvijen. Einstein je utvrdio zamjenjivost energije i mase i time proširio tumačenje zakona održanja energije, koji se danas obično navodi kao zakon održanja energije i mase.

U skladu s Einsteinovom teorijom, svaka promjena energije dE tijela povezana je s promjenom njegove mase dm formulom dE =dmc2, gdje je c brzina svjetlosti u vakuumu jednaka 3 x 108 Miss.

Iz ove formule, naime, proizlazi da ako se kao rezultat nekog procesa masa svih tijela koja sudjeluju u procesu smanji za 1 g, tada energija iznosi 9×1013 J, što je ekvivalentno 3000 tona standardno gorivo.

Ovi omjeri su od primarne važnosti u analizi nuklearnih transformacija. U većini makroskopskih procesa promjenu mase možemo zanemariti i govoriti samo o zakonu održanja energije.

Pratimo transformacije energije na nekom konkretnom primjeru. Razmotrite cijeli lanac pretvorbe energije potrebne za proizvodnju bilo kojeg dijela na tokarilici (slika 1). Neka je početna energija 1, čiju količinu uzimamo za 100%, dobivena potpunim izgaranjem određene količine fosilnog goriva. Dakle, za naš primjer, 100% početne energije sadržano je u produktima izgaranja goriva, koji su na visokoj (oko 2000 K) temperaturi.

Produkti izgaranja u kotlu elektrane pri hlađenju svoju unutarnju energiju predaju u obliku topline vodi i vodenoj pari. Međutim, iz tehničkih i ekonomskih razloga, produkti izgaranja ne mogu se ohladiti na temperaturu okoline. Oni se izbacuju kroz cijev u atmosferu na temperaturu od oko 400 K, odnoseći sa sobom dio izvorne energije. Stoga će se samo 95% početne energije prenijeti na unutarnju energiju vodene pare.

Rezultirajuća vodena para ulazi u parnu turbinu, gdje se njezina unutarnja energija najprije djelomično pretvara u kinetičku energiju struna pare, koja se zatim kao mehanička energija prenosi na rotor turbine.

Samo dio energije pare može se pretvoriti u mehaničku energiju. Ostatak se daje vodi za hlađenje kada se para kondenzira u kondenzatoru. U našem primjeru smo pretpostavili da će energija predana rotoru turbine biti oko 38%, što otprilike odgovara stanju stvari u modernim elektranama.

Pri pretvaranju mehaničke energije u električnu zbog tzv Joule gubici u namotima rotora i statora generatora će izgubiti oko 2% energije. Kao rezultat toga, oko 36% početne energije otići će u mrežu.

Električni motor će pretvoriti samo dio električne energije koja mu je dovedena u mehaničku energiju za rotaciju tokarilice. U našem primjeru, oko 9% energije u obliku Jouleove topline u namotima motora i topline trenja u njegovim ležajevima otpustit će se u okolnu atmosferu.

Dakle, samo 27% početne energije bit će isporučeno radnim organima stroja. No, energetskim nesrećama ni tu nije kraj. Ispostavilo se da se većina energije tijekom obrade dijela troši na trenje i u obliku topline odvodi s tekućinom koja hladi dio. Teoretski, samo vrlo mali dio (u našem primjeru, pretpostavlja se 2%) početne energije bio bi dovoljan da se dobije željeni dio izvornog dijela.

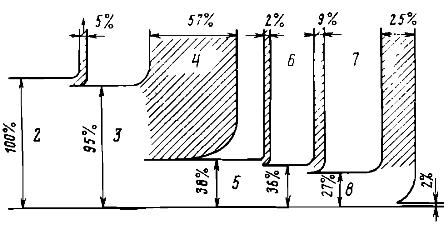
Riža. 1. Dijagram energetskih transformacija tijekom obrade izratka na tokarilici: 1 — gubitak energije s ispušnim plinovima, 2 — unutarnja energija produkata izgaranja, 3 — unutarnja energija radnog fluida — vodena para, 4 — toplina oslobođena hlađenjem. voda u kondenzatoru turbine, 5 — mehanička energija rotora turbogeneratora, 6 — gubici u elektrogeneratoru, 7 — otpad u električnom pogonu stroja, 8 — mehanička energija vrtnje stroja, 9 — trenje. rad, koji se pretvara u toplinu, odvojen od tekućine, rashladni dio, 10 — povećanje unutarnje energije dijela i čipsa nakon obrade ...

Iz primjera koji razmatramo mogu se izvući najmanje tri vrlo korisna zaključka, ako se smatra prilično tipičnim.

Prvo, u svakom koraku pretvorbe energije nešto se gubi... Ovu izjavu ne treba shvatiti kao kršenje zakona održanja energije. Gubi se zbog korisnog učinka za koji se izvodi odgovarajuća transformacija. Ukupna količina energije nakon pretvorbe ostaje nepromijenjena.

Ako se proces pretvorbe i prijenosa energije odvija u određenom stroju ili aparatu, tada se učinkovitost ovog uređaja obično karakterizira učinkovitošću (učinkovitošću)... Dijagram takvog uređaja prikazan je na si. 2.

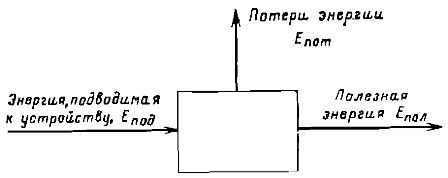
Riža. 2. Shema za određivanje učinkovitosti uređaja koji pretvara energiju.

Koristeći oznake prikazane na slici, učinkovitost se može definirati kao Učinkovitost = Epol/Epod

Jasno je da u ovom slučaju, na temelju zakona održanja energije, mora postojati Epod = Epol + Epot

Stoga se učinkovitost može napisati i na sljedeći način: učinkovitost = 1 — (Epot / Epol)

Vraćajući se na primjer prikazan na SL. 1, možemo reći da je učinkovitost kotla 95%, učinkovitost pretvaranja unutarnje energije pare u mehanički rad 40%, učinkovitost električnog generatora 95%, učinkovitost je — električni pogon a stroj — 75%, a učinkovitost stvarne obrade obratka je oko 7%.

U prošlosti, kada još nisu bili poznati zakoni transformacije energije, san ljudi bio je stvoriti takozvani perpetum mobile — uređaj koji bi obavljao koristan rad bez trošenja energije. Takav hipotetski motor, čije bi postojanje kršilo zakon o očuvanju energije, danas se naziva vječnim gibačem prve vrste, za razliku od vječnog gibanja druge vrste. Danas, naravno, nitko ne uzima ozbiljno mogućnost stvaranja perpetuum mobile prve vrste.

Drugo, svi gubici energije u konačnici se pretvaraju u toplinu, koja se ispušta ili u atmosferski zrak ili u vodu iz prirodnih rezervoara.

Treće, ljudi na kraju iskoriste samo mali dio primarne energije koja se troši za postizanje relevantnog blagotvornog učinka.

To je osobito vidljivo kada se promatraju troškovi transporta energije. U idealiziranoj mehanici, koja ne uzima u obzir sile trenja, pomicanje tereta u horizontalnoj ravnini ne zahtijeva energiju.

U realnim uvjetima sva energija koju vozilo potroši koristi se za svladavanje sila trenja i sila otpora zraka, odnosno u konačnici se sva energija potrošena u prometu pretvara u toplinu. S tim u vezi, zanimljive su sljedeće brojke koje karakteriziraju rad premještanja 1 tone tereta na udaljenosti od 1 km s različitim vrstama prijevoza: zrakoplov — 7,6 kWh / (t-km), automobil — 0,51 kWh / ( t- km) , vlak-0,12 kWh / (t-km).

Tako se isti povoljan učinak može postići zračnim prometom na račun 60 puta veće potrošnje energije nego željeznicom. Naravno, velika potrošnja energije daje značajnu uštedu vremena, ali čak i pri istoj brzini (auto i vlak), troškovi energije razlikuju se 4 puta.

Ovaj primjer sugerira da ljudi često rade kompromise s energetskom učinkovitošću kako bi postigli druge ciljeve, na primjer udobnost, brzinu itd. U pravilu, energetska učinkovitost samog procesa nas malo zanima — opće tehničke i važna je ekonomska procjena učinkovitosti procesa... Ali kako cijene primarnih energetskih komponenti rastu, energetska komponenta u tehničkim i ekonomskim procjenama postaje sve važnija.